Encyclopaedia Index

THE MATHEMATICAL BASIS OF PHOENICS

Contents

1. Purpose And Topics Covered
2. Variables
3. Storage
4. Grids
5. The Balance Equation
6. Parabolic Flows
7. Auxiliary Equations
8. Boundary Conditions

1. Purpose And Topics Covered

The aim of this lecture is to introduce the basic mathematical concepts behind PHOENICS. An overview of the solution algorithms used is given in a separate lecture.

Topics Covered

Variables

• What
• Where
• When

Equations

• Balance
• Auxiliary

Boundary conditions

2. Variables

Classification

Variables may be thought of as being:

• dependent - the subject of a conservation equation
• auxiliary - constant, or derived from an algebraic expression.

In each case, they can be further subdivided into scalar and vector quantities:

• Dependent:
  • Scalars:
    • Pressure
    • Temperature
    • Enthalpy
    • Mass fractions
    • Volume fractions
    • Turbulence quantities
    • Various potentials
  • Vectors:
    • Velocity resolutes
    • Radiation fluxes
    • Displacements
• Auxiliary:
  • Scalars:
    • Density
    • Viscosity
    • Conductivity
    • Diffusivity
    • Specific heat
    • Thermal expansion coefficient
    • Inter-fluid transport
    • Absorptivity
    • Compressibility
  • Vectors:
    • Various non-isotropic properties
    • Gravity forces
    • Other body forces

The quantities defining the problem geometry can also be divided into scalar and vector categories:

• Geometric:
  • Scalars:
    • Cell volumes
    • Volume porosity factors
    • Inter-fluid surface area per unit volume
  • Vectors:
    • Cell center coordinates
    • Cell corner coordinates
    • Center to center distances
    • Cell surface areas
    • Cell area porosities

3. Storage

The distinction between scalar and vector is important, because each is stored at a different location in space:

• Scalars - These are stored at the center points of six-sided cells, with values supposed to be typical of the whole cell.
• Vectors - These are stored at the center points of the six cell faces.

Nomenclature - A compass-point notation is used, as shown below

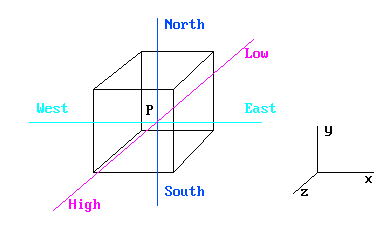
P = Cell center

N,S,E,W,H,L = Neighbour-cell centers

S -> N = Positive IY

W -> E = Positive IX

L -> H = Positive IZ

T = Cell center at previous time step 

An array of cells with the same IZ is referred to as a SLAB.

Steady or Transient

Steady-State Problems - PHOENICS can proceed directly to the steady-state solution. It is not necessary to march through time to reach the steady state.

Transient Problems - PHOENICS can cope with constant and variable time steps. The time step size can be a function of time.

4. Grids

Storage locations

Vector quantities are computed by reference to cells which are staggered with respect to the scalar cells.

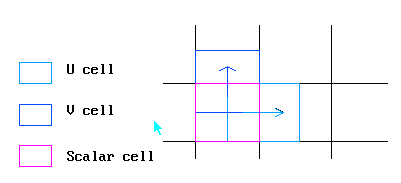
3 velocities and 1 scalar share the same cell index (IX,IY,IZ).

Any scalar or vector quantity can only be referenced by a unique (IX,IY,IZ) index. Thus the velocity on the West face of the cell P above 'belongs' to the West scalar cell.

Types of Grid

PHOENICS grids are structured - cells are topologically Cartesian brick elements.

PHOENICS grids may be :

• Cartesian
• Cylindrical-polar
• Body fitted, orthogonal or non-orthogonal

In all cases, the grid distribution can be non-uniform in all coordinate directions.

For cylindrical-polar coordinates, the following orientation is used:

• X (or I) is always the angular direction
• Y (or J) is always the radial direction
• Z (or K) is always the axial direction

5. The Balance Equation

Basic form

The basic balance, or conservation equation is just:

Outflow from cell - Inflow into cell = net source within cell

The quantities being balanced are the dependent variables from the earlier panel:

• mass of a phase
• mass of a chemical species
• energy
• momentum
• turbulence quantities
• electric charge etc.

Terms

The terms appearing in the balance equation are:

• Convection (i.e., directed mass flow)
• Diffusion (i.e., random motion of electrons, molecules or larger structures e.g., eddies)
• Time variation (i.e., directed motion from past to present - accumulation within a cell)
• Sources (e.g., pressure gradient or body force for momentum, chemical reaction for energy or chemical species)

The Generalized Form

The single phase conservation equation solved by PHOENICS can be written as:

where: φ - the variable in question

ρ - density

- vector velocity

- the diffusive exchange coefficient for f

- the source term

Particular Forms

Particular examples are:

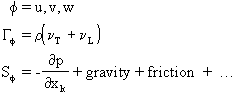Momentum

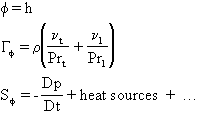Enthalpy

Continuity

where are the turbulent and laminar viscosities, and Pr_t, Pr_l are the turbulent and laminar Prandtl/Schmidt Numbers.

Numerical solution

The balance equations cannot be solved numerically in differential form. Hence, PHOENICS solves a finite-volume formulation of the balance equation.

The FVE's are obtained by integrating the differential equation over the cell volume.

Interpolation assumptions are required to obtain scalar values at cell faces and vector quantities at cell centers.

No Taylor series expansion or variational principle is used.

Finite Volume Form

After integration, the FVE has the form:

where:

(by continuity)

The neighbour links, the a's, have the form

convection diffusion transient

Correction Form

The equation is cast into correction form before solution.

In correction form, the sources are replaced by the errors in the real equation, and the coefficients may be only approximate. The corrections tend to zero as convergence is approached, reducing the possibility of round-off errors affecting the solution.

The neighbor links:

• Increase with inflow velocity, cell area, fluid density and transport coefficient
• Decrease with internodal distance
• Are always positive.

6. Parabolic Flows

Transient phenomena are always parabolic - the future cannot affect the past.

This allows for a marching solution, with only the current and previous time step values required. Reducing time step size thus does not increase memory requirements.

Steady-state flows can also be parabolic if the flow is unidirectional, and diffusion in that direction is negligible.

Solution can now be achieved by marching through space, with considerable saving in memory requirement. In PHOENICS, such marching is always in the Z (or K) direction.

7. Auxiliary Equations

To close the equation set, auxiliary equations must be provided for:

• Thermodynamic properties: density, (enthalpy, entropy)
• Transport properties: viscosity, diffusivity, conductivity
• Source terms: chemical kinetic laws, radiation absorption, viscous dissipation, Coriolis etc.
• Interphase transport: of momentum, energy, mass , chemical species etc.

There may also be 'artificial' auxiliary equations, such as

• False transients (for relaxation)
• Boundary conditions

All of the above may be functions of some or all of the other solved-for variables, or auxiliary quantities, resulting in a highly non-linear set of equations.

8. Boundary Conditions

Introduction

Another lecture in this series is devoted to Boundary Conditions in PHOENICS, so only a brief overview and introduction will be presented here.

Boundary Conditions can be:

• Fixed value
• Fixed flux
• Linear
• Non-linear

General form

Boundary Conditions are represented in PHOENICS as linearized sources for cells adjacent to boundaries:

a_BC is termed the COEFFICIENT.

is termed the VALUE.

a_BC is added to a_P , and is added to the RHS of the equation for .

Particular forms

For a fixed value boundary, a_BC is made very big. The effect is:

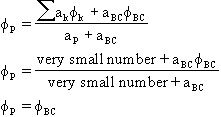
For a fixed flux boundary, a_BC is made very small, and is set to the required flux.

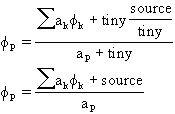
Linear and non-linear conditions can be set by appropriate prescription of a_BC and