Encyclopaedia Index

Linear Equation Solvers and Pre-conditioners in PHOENICS

Available solvers, Available Pre-conditioners, Activation - VR Editor, Activation - Q1 / PIL, Detailed Solver Control, Advice

Available Solvers

The following linear equation solvers are available:

1. STONE - default PHOENICS Stone-type solver, which does not use a pre-conditioner
2. CGRS - Conjugate-Gradient-Residual Solver
3. CNGR - PHOENICS's Conjugate-Gradient-Residual solver - with ILU0 or JACOBI pre-conditioners
4. MSIP - PHOENICS's MSIP
5. BCG - Bi-Conjugate Gradient Method
6. BCGSTAB - Bi-Conjugate Gradient Method stabilized
7. TFQMR - Transpose-Free Quasi-Minimum Residual method
8. FGMRES - Flexible version of Generalized Minimum RESidual method
9. DQGMRES - Direct versions of Quasi Generalize Minimum Residual method
10. AMG - BoomerAMG from HYPRE, which does not use a preconditioner
11. HBiCGStab - BiCGStab from HYPRE
12. HGMRES - GMRES from HYPRE
13. HFlexGMRES - FlexGMRES from HYPRE
14. HLGMRES - LGMRES from HYPRE

Note that in parallel, the STONE, CNGR and MSIP solvers are replaced by a parallel version of the CGRS solver. The remaining solvers operate in serial and parallel modes.

Further, the CNGR and MSIP solvers should not be used for the energy equation when there are conjugate cut cells present.

The default PHOENICS solvers (Stone, CNGR and MSIP) always solve all variables in all cells, including blocked (PRPS>=100) and non-participating (PRPS=198,199) cells. All the other solvers only solve in cells which are 'live' for that variable. Thus the velocity and turbulence equations are only passed into the solver for fluid cells, whereas the energy equation is solved in all participating cells, fluid and solid.

In parallel, the default PHOENICS solvers split the domain between processors to produce a similar number of cells on each processor. If there is a large number of blocked cells, this may lead to poor load balancing between the processors. All the other solvers include a load-balancing algorithm which will attempt to place an equal load on each processor for each variable. The improved load balancing comes at the cost of additional data transfer before and after solving. The load balancing algorithm can be turned off by setting the allowed imbalance ratio to be very large:

SPEDAT(SET,BALANCE,PARALL,R,1E6)

The number of active cells for each variable and the split between processors for parallel are reported at the top of the RESULT file.

Available Pre-conditioners

The following preconditioners are available:

1. NONE - preconditioner is absent
2. PBP - point-by-point preconditioner
3. Jacobi - iterational Jacobi preconditioner (CNGR only)
4. ILU0 - simple ILU(0) preconditioning (CNGR only)
5. AMG - BoomerAMG as preconditioner from HYPRE
6. ParaSail - ParaSail from HYPRE
7. Euclid - Euclid from HYPRE
8. PILUT - PILUT from HYPRE

Note that not all preconditioners are available for all solvers. The Stone, MSIP and AMG solvers do not require a preconditioner.

The HYPRE solvers can only use PBP or HYPRE preconditioners.

The Jacobi and ILU0 preconditioners are only available for the CNGR solver, which itself is only available in sequential mode.

Activation - VR Editor

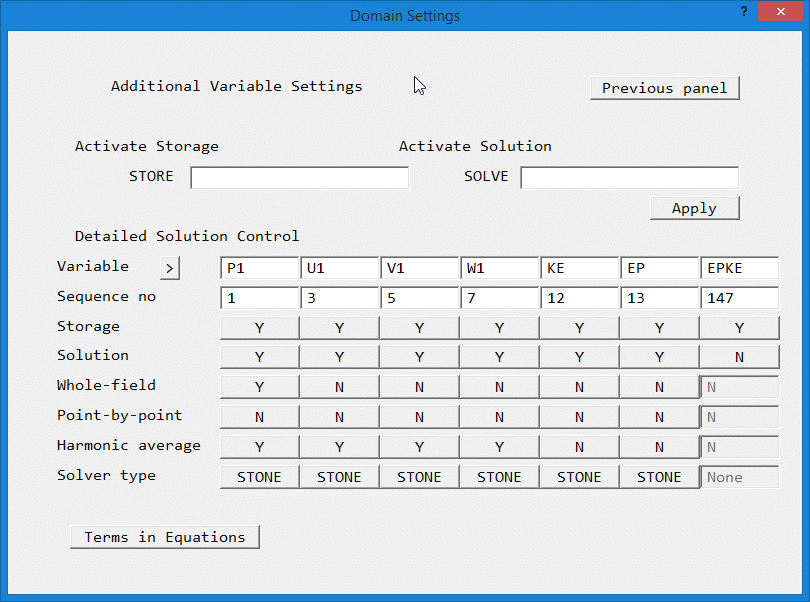
In the VR Editor, the solvers and pre-conditioners are selected from Main Menu - Models - Solution control / Extra variables

The 'Solver type' buttons allow a different solver / pre-conditioner to be selected for each variable.

Activation - Q1 / PIL

In the Q1 file, the solvers and pre-conditioners are held in SPEDAT commands in Group 19. If there are no such settings, the STONE solver will be used for all variables. The setting ENDIT(var)=GRND1/2 is still interpreted as meaning that the conjugate-gradient solver should be called or that variable, and CSG3=CNGR as meaning it should be used for all variables.

The full range of solvers can be activated for all variables by the command:

SPEDAT(SET,LES,SOLVER,I,iSolver)

where iSolver is an integer denoting the solver to use. Similarly, the pre-conditioner to use for all variables is set by:

SPEDAT(SET,LES,PRECOND,I,IPrecond)

To set the solver and pre-conditioner for an individual variable, use:

SPEDAT(SET,SOLPHI,ivar,I,iSolver)
SPEDAT(SET,PREPHI,ivar,I,iPrecond)

The values of iSolver are as follows:

The values of iPrecond are as follows:

The VR Editor will read the above SPEDAT commands and display the appropriate dialogs. On exit, it will create new SPEDAT commands based on the current choice(s)

Detailed Solver Control

These settings, which must be edited into Group 19 of the Q1 file, are applied to all variables for which the solver is used. More details can be found in the HYPRE documentation.

1. AMG
   • SPEDAT(SET, AMG, PRINTLEVEL, I, 0)
     1 for some output, 2 for more and 3 or larger for full output to command line.
   • SPEDAT(SET, AMG, COARSENTYPE, I, 8)
     Coarsening type 8 “PMIS” has smallest memory footprint & is nominally fastest
   • SPEDAT(SET, AMG, RELAXTYPE, I, 6)
     Relaxation type 6 is symmetric hybrid-Gauss-Seidel, 3 is forward non-symmetric hybrid-Gauss-Seidel and 4 is backward non-symmetric hybrid-Gauss-Seidel. 6 is more slightly more expensive, but seems to be a better smoother especially for P1.
   • SPEDAT(SET, AMG, INTERPTYPE, I, 6)
     Haven’t tried these.
   • SPEDAT(SET, AMG, NUMSWEEPS, I, 2)
     2 sweeps seem to be a good speed vs effectiveness compromise.
   • SPEDAT(SET, AMG, PREMAXITER, I, 1)
     Max iterations when used as a pre-conditioner
   • SPEDAT(SET, AMG, MAXITER, I, 10)
     Max iterations when used as a solver
   • SPEDAT(SET, AMG, STRONGTHRSHLD, R, 0.10)
     Threshold below which to drop connections in the coarse level coefficient matrix. A lower value produces are sparser coarse level and is often faster.
   • SPEDAT(SET, AMG, AGGNUMLEVELS, I, 1)
     AMGs first level on Cartesian grids leads to a lot of fill-in, this can be avoided by applying aggressive coarsening to the top level.
2. ParaSails
   • SPEDAT(SET, PARASAIL, PRINTLEVEL, I, 0)
     Anything other than 0 produces some output to command line.
   • SPEDAT(SET, PARASAIL, LEVEL, I, 1)
     ?
   • SPEDAT(SET, PARASAIL, THRSHLD, R, 0.1)
     ?
   • SPEDAT(SET, PARASAIL, FILTER, R, 0.1)
     ?
   • SPEDAT(SET, PARASAIL, SYM, I, 0)
     ?
3. Euclid
   • SPEDAT(SET, EUCLID, PRINTLEVEL, I, 0)
     Anything other than 0 produces some output to command line.
   • SPEDAT(SET, EUCLID, LEVEL, I, 1)
     Number of levels of fill-in. If A has 7 diagonals, ilu(0)’s L has 4 and U has 3 diagonals (plus the main diagonal full of ones). If you were to multiply L by U you would not get a matrix with 7 diagonals, but instead one with 13 diagonals. ilu(1) corresponds to permitting the factorisation to have entries in these 13 diagonals instead of just 7.
   • SPEDAT(SET, EUCLID, BJ, I, 1)
     Switch between “Parallel” and block-Jacobi ilu (also parallel). When speed is important and not robustness, especially cause we only solve to moderate tolerances, block-Jacobi is preferred.
4. PILUT
   • SPEDAT(SET, PILUT, NNZ, I, 7)
     Number of non-zero entries per row of the factorization. For a matrix A with 7 diagonals, nnz=13 would be the same as Euclids ilu(1).
   • SPEDAT(SET, PILUT, THRSHLD, R, 0.01)
     Tolerance below which to drop entries from the factorization.

Individual SPEDATs

Individual solver settings for a variable can currently also be made using the following SPEDATs, overwriting the defaults or any global settings made using the above SPEDATs. 'ivar' is the variable to be affected, e.g. P1, U1,... TEM1,...

SPEDAT(AMGPRL,ivar,I,1)    AMG Print Level
SPEDAT(AMGCOT,ivar,I,8)    AMG Coarsening Type
SPEDAT(AMGRET,ivar,I,6)    AMG Relaxation Type
SPEDAT(AMGINT,ivar,I,6)    AMG Interpolation Type
SPEDAT(AMGNSW,ivar,I,2)    AMG Number of Sweeps
SPEDAT(AMGPMI,ivar,I,1)    AMG Preconditioner Maximum Iterations
SPEDAT(AMGSMI,ivar,I,1)    AMG Solver Maximum Iterations
SPEDAT(AMGTHR,ivar,R,0.1)  AMG Strong Threshold
SPEDAT(AMGNAL,ivar,I,1)    AMG Number of Aggressive Coarsening Levels
SPEDAT(PASPRL,ivar,I,1)    ParaSails Print Level
SPEDAT(PASNLV ivar,I,1)    ParaSails Level
SPEDAT(PASTHR ivar,R,0.1)  ParaSails Threshold
SPEDAT(PASFIL ivar,R,0.1)  ParaSails Filter
SPEDAT(PASSYM ivar,I,1)    ParaSails Symmetry
SPEDAT(EUCPRL ivar,I,1)    Euclid Print Level
SPEDAT(EUCNLV ivar,I,0)    Euclid Number of Levels of fill-in
SPEDAT(EUCPBJ ivar,I,1)    Euclid Block-Jacobi mode
SPEDAT(PILUNZ ivar,I,7)    PILUT Number of Non-Zero entries per row of factorization
SPEDAT(PILUTH ivar,R,0.01) PILUT Threshold for dropping fill-in from factorization 

Advice

The existing STONE and CNGR solvers are very robust and reliable. However, they lose efficiency as the number of cells increases. They also have to solve over all cells in the domain, regardless of whether the cell is blocked or not. When a large proportion of the cells is blocked, convergence of the solver may be adversely affected. In parallel, load balancing may be hard to achieve.

The new solvers and pre-conditioners differ in that they only load 'live' cells into the solver matrix. This can greatly reduce the workload of the solver, at the expense of having to copy coefficients into the solver matrices, and then to copy the solution out. There is also a load balancing algorithm for parallel operation which ensures that all processors have to solve approximately the same number of equations regardless of the blockage distribution.

The new solvers, especially the ones from HYPRE are less affected by grid refinement, and should prove superior for fine grids, especially when there are many blocked cells.

Based on the rather limited experience to date, it is advised to use the following combinations of solver and pre-conditioner:

• Pressure correction - AMG or CGRS+AMG
• Velocity - CGRS+PBP
• Energy - CGRS+AMG or AMG
• LTLS - AMG