contents

The lecture explains:

• what it is,
• how it works
• its current limitations, and
• how it can be improved.

The lecture is intended for experienced users of PHOENICS or other computer codes who understand what is meant by 'convergence' and 'divergence', and who know that ensuring the former and avoiding the latter are sometimes difficult.

Contents

1. What is CONWIZ?
2. Why is it needed?
3. How is it activated?
4. Examples of CONWIZ in action
5. How does it work?
6. How reliable is it?
7. Can users participate?
8. How can it be further developed?
9. The ideas underlying CONWIZ
10. How to monitor convergence
11. How to activate the new features
12. Future challenges for CONWIZ

start lecture, abstract or contents

1. What is CONWIZ?

The PHOENICS user who invokes it therefore has no need to set:-

• 'initial guesses', expressed for example by FIINIT-settings even when the problem is not time-dependent;
• relaxation factors, either 'linear' or 'false-time-step, via RELAX;
• upper and lower limits of variables, via VARMAX and VARMIN;
• increment limits, or
• other convergence-promoting devices.

He or she can therefore devote full attention to:-

• specifying correctly the geometrical and physical input data; and
• displaying and interpreting the physical results.

CONWIZ thus reduces worry and improves performance.

2. Why is CONWIZ needed?

• their large size,
• their non-linearity, and
• the inter-linkages between solved-for variables.

For example:

• all velocity components and density are linked via mass conservation;
• pressure is linked to them via momentum and thermodynamic principles;
• flow produces turbulence which causes flow-affecting momentum exchanges;
• non-uniformities of temperature both are propagated by fluid flow and affect that flow via buoyancy;
• and so on.

The governing equations enable the errors associated with a particular set of velocities, etc, to be computed. The question is then: what corrections should be made to their values so as to reduce the errors? Well-known solution strategies exist for solving the pressure-velocity-linkage problem, for example SIMPLE and its variants.

However, these involve 'relaxation parameters' which significantly affect the speed with which the errors are reduced, and even whether they are reduced at all.

In PHOENICS, these parameters are set by way of commands in the input file such as:

RELAX(DEN1, LINRLX, 0.5), for relaxing density,or
RELAX(U1, FALSDT, 1.e-3), for relaxing velocity.

However, although numerous examples of such settings are provided in the Input-File Library, little systematic advice has been given about:

• when to use LINRLX and when FALSDT, and
• how the numerical third argument of the command is to be selected.

The latter point is particularly troublesome when the FALSDT mode is used; for the third argument has the dimensions of 'time'; so the appropriate value is probably related to the speed at which events will take place in the flow; but it has to be chosen before the flow has been calculated.

Moreover, experience has shown that, for many problems, 'linear relaxation doesn't work' for velocities; so FALSDT has had to be used.

Inexperienced users have then sometimes chosen excessively small values of false-time-step, for example 1.e-6; and they have then mistakenly supposed that they had obtained converged solutions because the resulting sweep-to-sweep changes were extremely small.

In the early years of CFD, when its users were mainly specialists in the subject, such lack of guidance was perhaps tolerable, Now that CFD codes are being used by specialists in other subjects, not even good guidance is sufficient: the computer code should choose the convergence-promoting settings on its own.

It is to enable PHOENICS to attain this degree of self-sufficiency that CONWIZ has been introduced. It is as yet a novice 'wizard'; but it is learning fast.

3. How CONWIZ is activated

However, to activate CONWIZ is easy: all that is needed is the line:

CONWIZ = T

in the Q1 file; and there is an easier-to-remember setting which will be described below.

If the user has already made his or her own settings of relaxation parameters, (most of) these will be respected by CONWIZ (but not false time steps for velocities).

Therefore, if it is desired to 'leave it all to CONWIZ', these settings should be de-activated.

These settings can also now be made by way of the 'numerics' panel of the VR-Editor menu.

4. Examples of CONWIZ in action

Library case 274: flow around a van

The discussion will be based on the two figures displayed by clicking below, standard above and conwiz below:

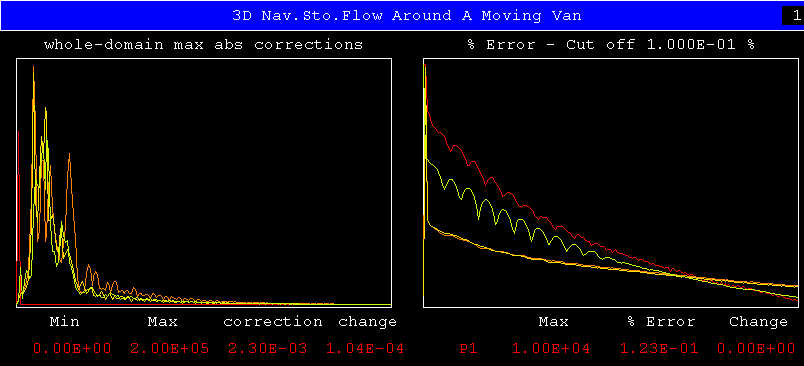
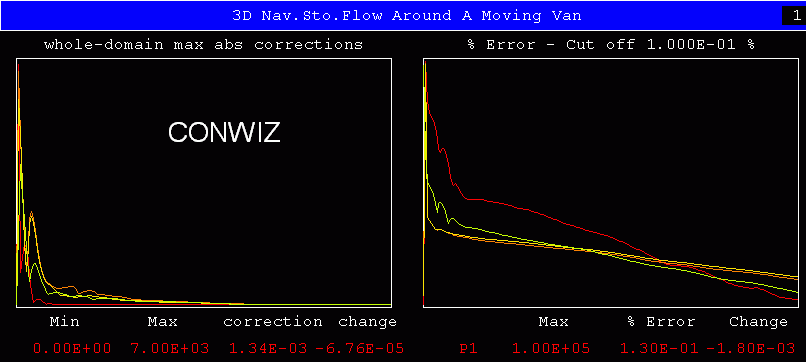
These show the graphical-monitor outputs for two runs with the same geometrical and physical inputs, but with convergence-influencing settings which differ in that:

• the first are those of the standard library case; and
• the second are those made by CONWIZ.

When considering these, it is should be noted that the left-hand plots are not those of the until-now-conventional 'spot values'; instead, the quantities plotted are, for each solved-for variable, the 'whole-domain maximum absolute corrections'.

These should, for a converged solution, fall to acceptably small values; as indeed they do in both cases here.

Convergence, as judged by this criterion, is therefore satisfactory both for the standard and the CONWIZ settings.

More rapid convergence is not to be expected of CONWIZ; indeed, when comparison with long-ago-optimised standard settings is made, somewhat slower convergence is more probable; for CONWIZ makes conservative rather than optimal choices.

Obviously, however, this play-safe policy has led to no serious ill-consequence in the present case.

The next two monitor plots show what happens when the van velocity is multiplied by 100.0 . As before, and for all pairs of pictures below, the standard settings are above and those of conwiz below.

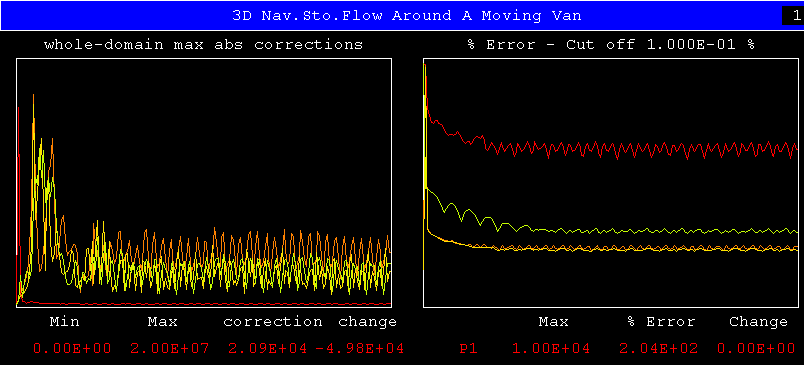
Evidently, the 'standard settings' which procured convergence for the original case were not able to do the same for the increased velocity; CONWIZ, by contrast, was able to cope with the changed input data quite well.

Library case 492; the gas-turbine combustor

Once again, the effects of the standard and CONWIZ settings are compared by way of the graphical-monitor plots which may be displayed by clicking below:

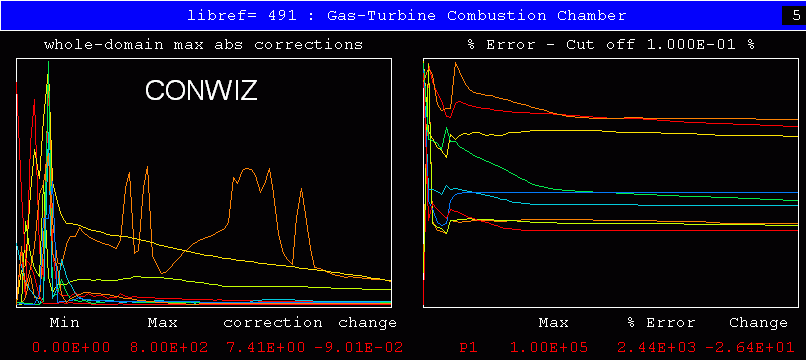
This time, the slower convergence of CONWIZ is more noticeable. However, it is gratifying to observe that convergence gas been achieved, with
CONWIZ = T
as the only setting which the user has had to make.

It should also be remarked that, although the maximum absolute corrections appear to fluctuate more wildly for CONWIZ, their actual values are extremely small.

Library case w802; the nuclear steam generator

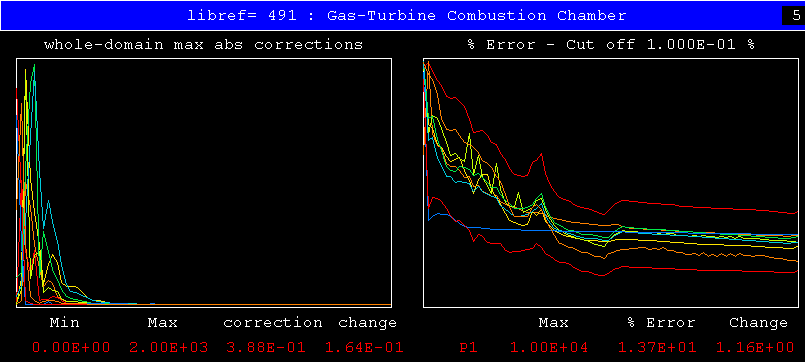
This is the nuclear steam generator, which was the application which, long ago, led to both to the invention of the IPSA algorithm and to the creation of PHOENICS itself.

CONWIZ is being asked to tackle this problem without even being given a hint (by way of FIINIT(STEAM) ) about the expected volume fractions of steam and water in the generator.

The next two pictures show the relevant monitor plots:

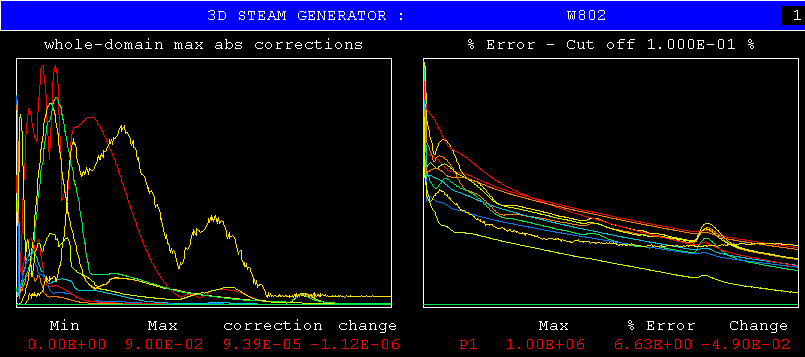
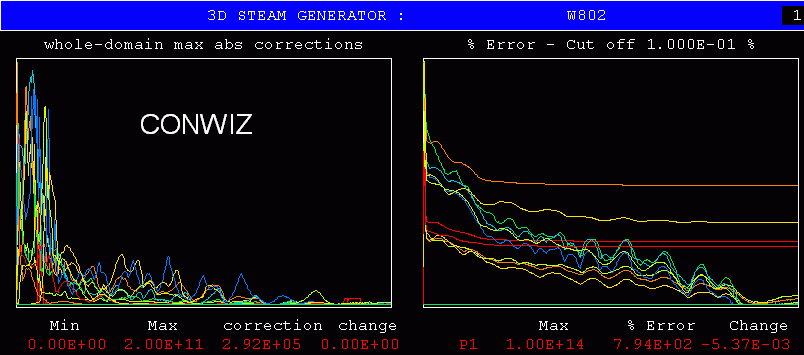
"Not bad for a beginner", one might conclude; although the levelling-off of some residuals requires examining.

Since the selection of relaxation parameters for two-phase flow is notoriously difficult, this first-time success of CONWIZ is especially encouraging.

Library case b524; the Mizuki impeller

The results, for the veteran Mizuki-impeller problem, are shown in the next two graphical-monitor plots:

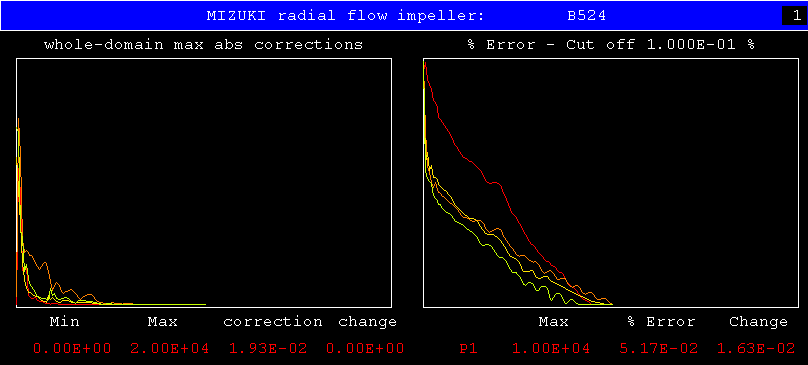
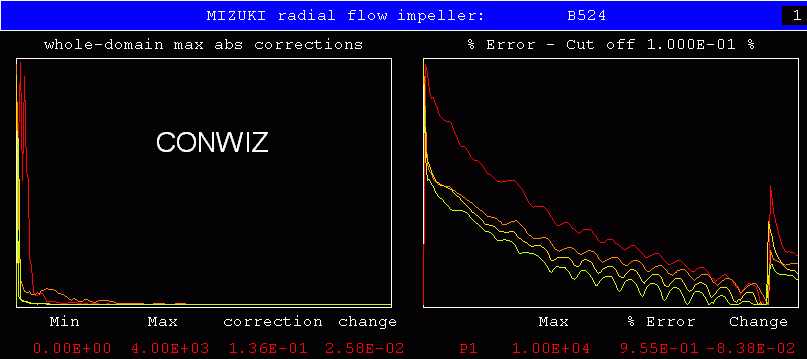
Convergence is good for both the standard and the CONWIZ settings; but the episode at the end of the CONWIZ run raises the question: why?

[However, this question is as much about the credibility of the residual plots as it is about the success of CONWIZ.]

Also interesting is what happens when the rotation speed is increased tenfold. This is shown by the next pair of plots:

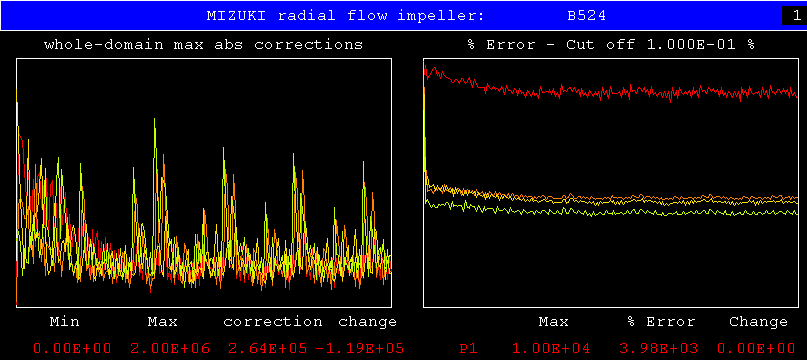
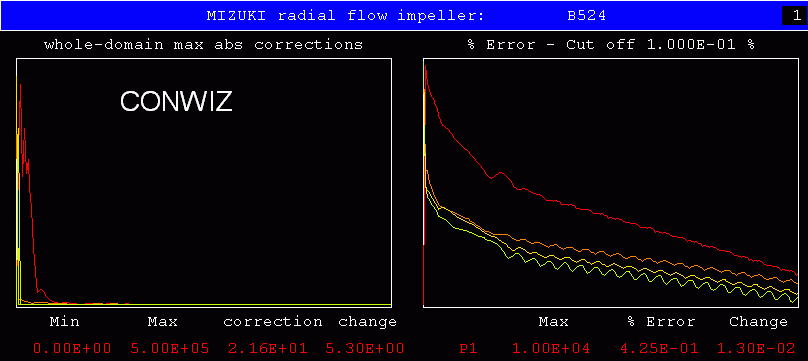
Evidently, CONWIZ handles the change without difficulty; but the 'standard' settings no longer procure convergence.

Library case i205; temperatures in a computer room

• the vertical-direction velocity
• the horizontal velocities
• the temperature

The next two pictures provide some encouraging evidence in respect of library case i205:

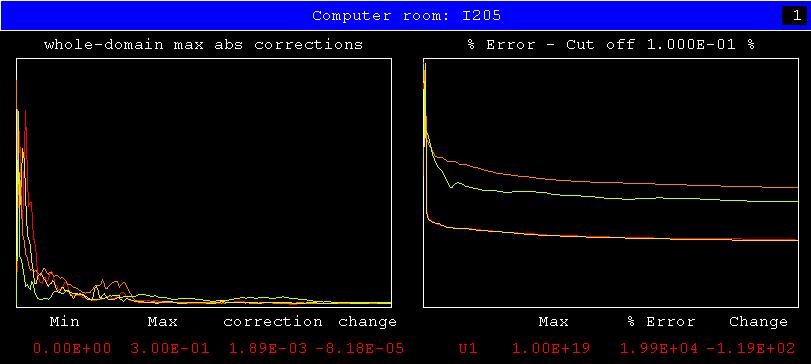
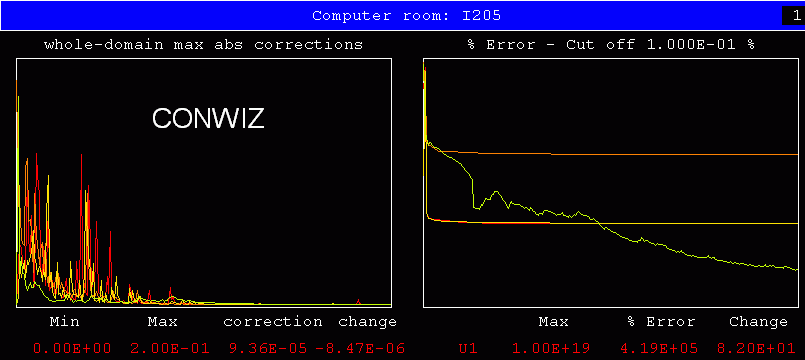
It appears that CONWIZ performs quite as well as the standard settings,

5. How does CONWIZ work?

1. It starts by making guesses about 'reference values' of:
   • length,
   • velocity,
   • density and
   • temperature.
2. From these it deduces and sets some initial values of variables, including the 'DVELDPs', i.e. the rates of change of velocity with pressure difference at every point.
3. It sets linear under-relaxation factors for all variables, including the DVELDPs .
4. It sets maximum values to the increments per sweep for some variables.
5. In some circumstances, it can improve its settings in the course of the computation.

6. How reliable is CONWIZ?

When CONWIZ has failed to procure complete convergence, it has sometimes transpired that there is some special instability promoter in the way in which the problem has been set up.

Fires represented as fixed heat sources regardless of flow conditions have led to solutions which not even CONWIZ can persuade to 'settle down'.

CONWIZ has been in existence only since February 2004, and has not been receiving full-time attention; too much should therefore not yet be claimed for it.

Nevertheless, to set CONWIZ=T is certainly a wise thing to do at the start of a new calculation.

7. How can users participate in the promotion of convergence?

If users prefer to use false-time-step relaxation, for any variable other than velocity, CONWIZ will print a message questioning their wisdom; but it will not change the settings.

It will however insist on using linear relaxation for velocities.

Any user-set linear-relaxation factor will be used in preference to its own.

User-set VARMINs and VARMAXs will also be respected (even if, being too narrowly defined, they distort the final solution).

Probably the best thing a user can do in order to help CONWIZ in cases of difficulty is to use the new maximum-absolute-correction limitation, by placing in the Q1 file such lines as:
SPEDAT(MAXINC,TEM1,R,user-set value)

This limits the maximum correction of temperature at any point in a singe sweep to the prescribed user-set value.

The user can also instruct CONWIZ to start from user-specified 'reference values' by way of the following commands:

SPEDAT(RLXFAC,REFVEL,R,user-set value)
SPEDAT(RLXFAC,REFLEN,R,user-set value)
SPEDAT(RLXFAC,REFTEMP,R,user-set value)
SPEDAT(RLXFAC,REFRHO,R,user-set value)

Further, if he or she is bold enough to use them, further spedats will set upper and lower limits, and relaxation factors, for the individual DVELDPs.

This is however not advised. 'Leave it to the wizard' is the better rule to follow.

8. How can CONWIZ be further developed?

1. By systematically inspecting all geometry-affecting settings, and all boundary and (physically significant initial) conditions, so as to make better estimates of reference lengths, velocities and densities.

2. By increasing horizontal-direction vertical-velocity coefficients in regions where un-balanced horizontal gradients of gravity are likely to provoke large vertical-velocity corrections.

3. By detecting regions in which corrections exhibit periodicity, and applying appropriate damping.

4. By examining the special features of body-fitted coordinates and of two-phase flow, and introducing such modifications to the DVELDPs as are appropriate.

5. Allowing better for low-Reynolds-number effects.

9. The ideas underlying CONWIZ

• SIMPLE-type CFD algorithms differentiate the momentum equations to deduce:
  DVELDP = AREA / [(sum of CONVCOs) + MASS / (DT + DTF) ]

• In steady-flow problems the true time step, DT, equals 0;

• at the start, convection coefficients (CONVCOs) may be 0;

• so a finite false time step, DTF, is needed to keep DVELDP finite; and so to prevent small pressure differences from producing enormous velocities;

• but these are not needed once CONVCOs are finite because motion has started;

• the much-used constant-DTF relaxation is thus now recognised as intrinsically bad; it should no longer be used.

• An initial DTF should be based on an initial estimate of what the CONVCO sum will be; then linear-under-relaxation allows the momentum-equation-based values to take over gradually.

• The fact that PHOENICS users have been successfully using constant-DTF strategies for a long time demonstrates the essential sturdiness of SIMPLE.

• Nevertheless, if any DTF is to remain in use, it should be deduced (by CONWIZ, of course) from local flow conditions and be based on monitored convergence behaviour.

• The same is true of other variables than velocity, except that the 'initial estimates' are harder for CONWIZ to make.

• For this reason, limitation of the size of the correction which may be made in any sweep provides a safer strategy.

These are the thoughts which underlie the strategies which CONWIZ currently employs; but the thinking is far from being completed.

10. How to monitor convergence

This is much more informative than the longer-established 'spot-value' mode; for how can one know in advance which are the important 'monitoring spots'?

Moreover, not only have 'spot-values' fallen into disfavour, but the suspicion has grown that the equally long-established 'residual' plots may be misleading, especially towards the end of run.

It has become apparent that the computed sum of residuals may include a large contribution from cells for which the balance is already as good as the round-off error of the computer allows.

This practice has two ill-effects, namely:

1. it causes a solution which has truly converged to appear to the user as though it has not; and
2. it causes the calculation process to continue to produce never-diminishing corrections which have no more significance than 'noise'.

Some experience has been gained with a procedure for filtering out quantitatively-insignificant residuals, with very satisfying results (the sums of residuals do truly reduce to zero); but this has not yet been tested sufficiently for general release.

It should be remarked that watching the maximum absolute corrections is of especial value when one finds that some of them do not fall to acceptably low values. For this is a sign that something may be wrong with the problem set-up (or, of course, with PHOENICS!)

PHOENICS has means of printing out ( when debug = T ) not only how big are the maximum absolute corrections for each variable, but also where they occur. Its use points out where the investigation of the problem can usefully begin.

It may be remarked that the CONWIZ project has valuably revived scrutiny of the calculation schemes employed by PHOENICS.

11. How to activate the new features

For example, at the bottom of the q1 for the case-274 calculation are the lines shown here.

The keywords 'conprom', 'endpause', 'maxabs' and 'figure' are comparatively easy to remember. Two of them are the same as those used in the cham.ini file, which now however users need not bring into their working directories for editing

Since the provision of such aids to memory is something which any user can do for himself, it may be of interest to explain the mechanism, as follows:

1. the new keyword has to be defined in the core input-library file 014.htm, wherein it will be seen that 'conprom', for example, is:
   • declared as a character variable, and
   • set equal to $056 .

2. the corresponding input-library file 056.htm has to be created, wherein the setting of CONWIZ is made.

   Similarly, library files 052.htm, 053.htm, 053.htmand 055.htm make corresponding settings.

These examples illustrate how PHOENICS users who are willing to hand-edit Q1 files can create short-cuts for themselves.

However, lest processing the files by way of the VR-Editor should wipe them out, they are best protected by informbegin and informend markers.

Note that in the VR-Editor CONWIZ is controlled from the Main Menu / Numerics / Relaxation Control panel. The choice of convergence monitor plot is made from the Options / Solver Monitor Options pull-down menu.

12. Future challenges for CONWIZ

For example, solid stresses and strains can be deduced from displacements, which PHOENICS has been taught to compute in the same manner in which it computes velocities. Yet it is highly improbable that the optimum convergence strategies will be the same for both.

Further, some solid objects may move relative to each other.

For example, a bat may collide with a slightly flexible ball, having dramatic effects on the air which is squeezed between them.

CONWIZ may have to rise to new heights of wizardry if, as is essential, the PHOENICS user is to be freed from worry about how to procure convergence.

Further, the introduction of the 'Complete PHOENICS Object' concept will make it possible for users to set up extremely complex problems with ease. CONWIZ will have to cope with all of them.

It may thus be concluded that CONWIZ has appeared just in time; for, without it, these new facilities might in practice prove impossible to use.