MULTI-PHASE-FLOW SIMULATION in PHOENICS

1. Definitions
2. IPSA for two inter-penetrating continua
3. multiple inter-penetrating continua
4. separated (i.e.free-surface) flows
5. the Lagrangian (i.e.particle-group tracking option)

1. Definitions

Examples are:-

• suspensions of oil droplets in water, or of water droplets in oil;
• the air-snow mixture in an avalanche;
• the sand-air mixture in a sandstorm;
• the "mushy zone" of mixed solid and liquid metal in a casting mould;
• the water-air mixture in a shower bath;
• the gas-oil-water mixture, in the pores within rock, in a petroleum-recovery process;
• droplets of fuel oil, mixed with hot gases, in a combustion chamber.

Definition of a phase
The above examples employ the word "phase" in the sense customary in thermodynamics, where the liquid, solid and gas phases are distinguished.

However, a broader definition of phase is used in PHOENICS. This allows sand particles of different densities, or steam bubbles of different sizes, or gas eddies of different temperatures, also to be regarded as different phases.

The distinction between intermingled and separated multi-phase flows

Often, the multiple phases in the complete domain become sharply separated. This happens, for example, when the gas flame beneath a domestic kettle is switched off; for the bubbles rise, the suspended droplets fall, and a plane unbroken surface forms between the steam and the water.

The flow is then often called a fully-separated or free-surface flow.

Both intermingled and separated flows are considered in this encyclopaedia article.

Simulation methods in PHOENICS

1. as two inter-penetrating continua, each having at each point in the space-time domain under consideration, its own:
   • velocity components,
   • temperature,
   • composition,
   • density,
   • viscosity,
   • volume fraction,
   • etc;
2. as multiple inter-penetrating continua having the same variety of properties;
3. as two non-interpenetrating continua, separated by a free surface; or
4. as a particulate phase for which the particle trajectories are computed as they move through a continuous fluid.

Method (1) IPSA for two inter-penetrating continua.

Method (2): multiple inter-penetrating continua: (the algebraic-slip method)

When many phases are present, it is impractical to solve full sets of Navier-Stokes equations for all of them.

In this method, therefore, only one set of differential equations is solved, to give the mixture-mean velocities at each point and time.

Then separate sets of equations are solved, one for each phase, which govern its relative velocities, i.e.their differences from the mean.

The latter equations are algebraic ones, which are derived from the Navier-Stokes equations by neglect of second-order terms.

This entails that the relative velocities are computed by reference only to the local pressure gradients, the body forces and the inter- phase friction.

The volume fractions occupied by each phase, at each point and time, are calculated at the same time.

This method is referred to in the PHOENICS documentation as the "algebraic-slip" method, with the abbreviation ASLP. Elsewhere in the scientific literature, it is sometimes called the "drift-flux" method.

It is embodied in the Advanced Multi-Phase Flow option of PHOENICS; and it makes use of the open-source Fortran file GXASLP.FOR .

Click here for a lecture on the algebraic-slip method

This method is especially useful for simulating sedimentation and other processes, for example the separation of oil, gas and water in a centrifuge.

An example of this kind now follows.

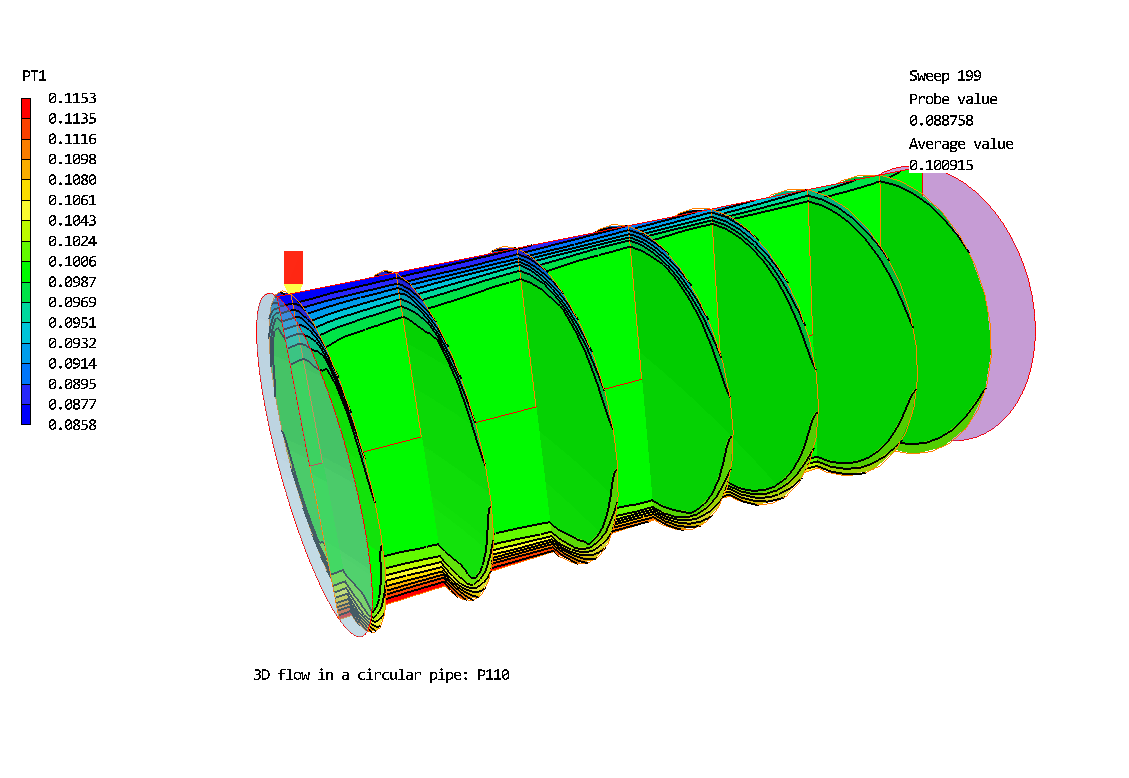
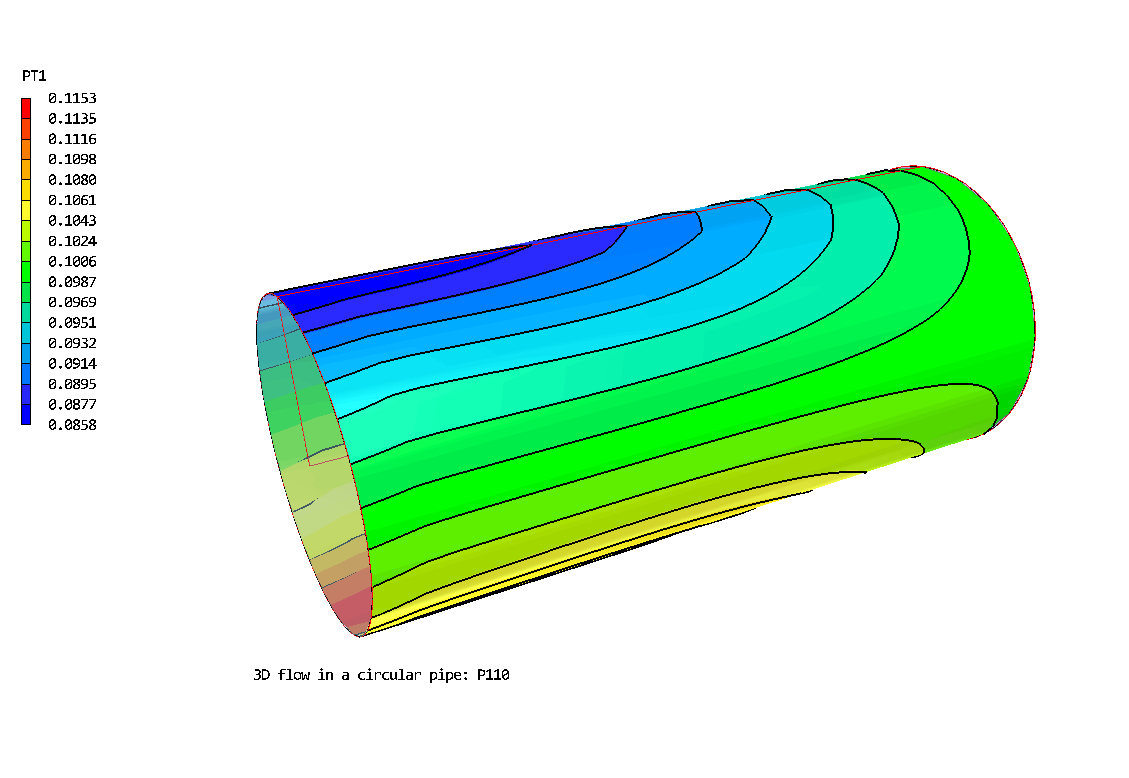
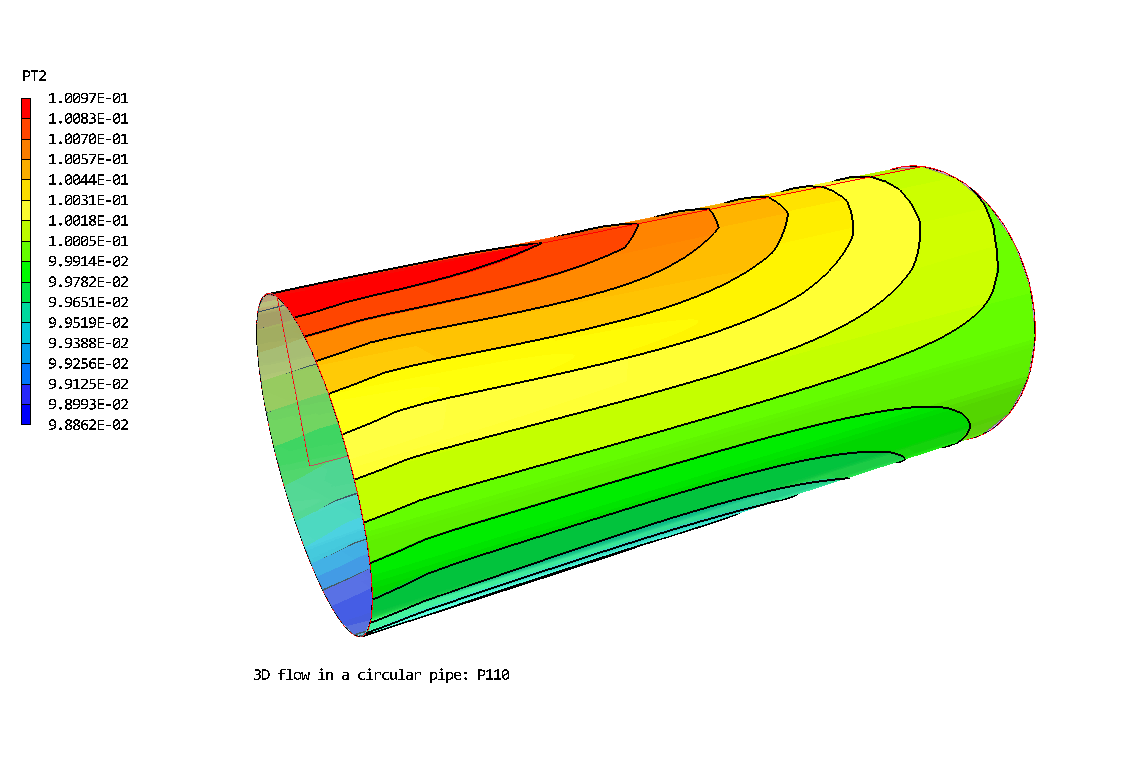
The 3D Polar grid: 20 * 20 *30. Flow is from left to right. The geometry has been expanded by a factor of 5 in the radial direction.

• The case calculates the accumulation of two groups of particles of different diameters along the bottom of a circular pipe. The carrier fluid has a density of 1000kg/m³, the particle density is 2000 kg/m³. The larger particles have a diameter of 1.0E-4m, the smaller ones 2.0E-5m.
• The Algebraic Slip Model is used to solve this problem.
• Slip velocities are normal to the continuous phase flow direction.
• Larger particles fall to the bottom more quickly than the smaller ones.
• This forces the liquid to rise up bringing the smaller particles with it.

Contours of pressure

Contours of the larger-diameter (particle air concentration

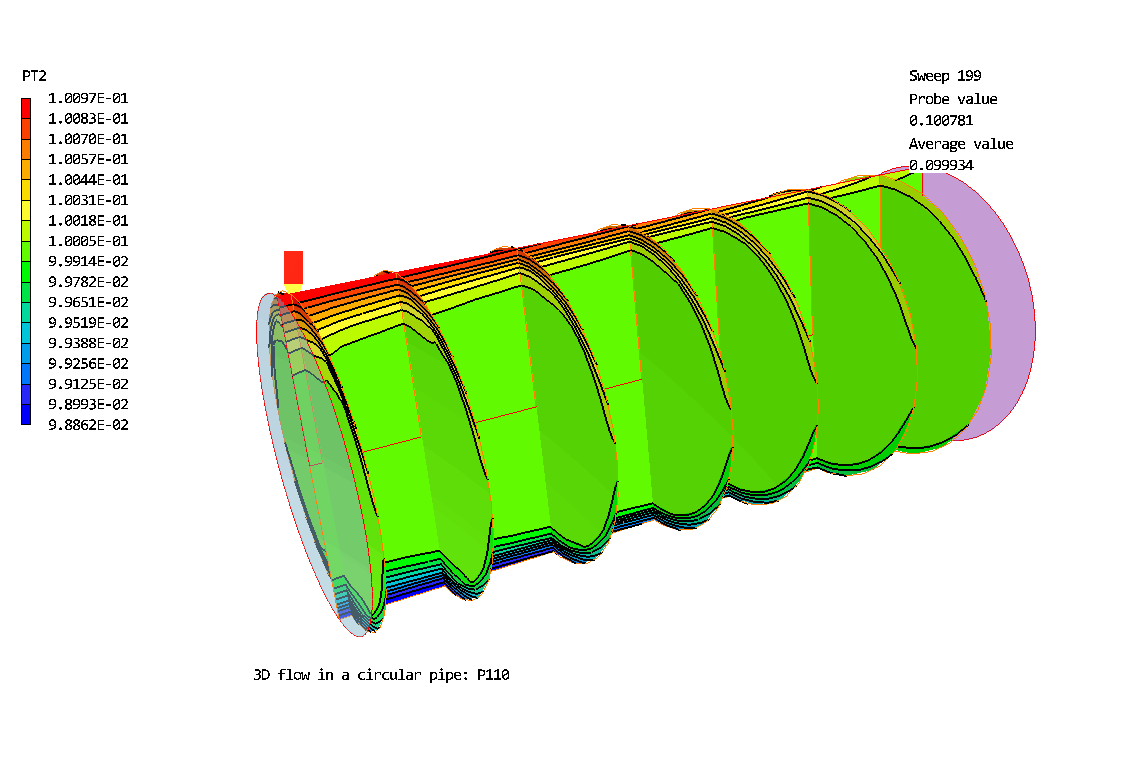
Contours of the smaller-diameter particle air concentration

See also the following Applications Album entry

Method (3): Separated (i.e.free-surface) flows

Method (3) treats the two (or more) fluids as a single fluid subject to discontinuities of density, viscosity and composition.

These discontinuities, i.e.the inter-fluid surfaces, are tracked as they move through the domain of interest, by solution of the individual continuity equations of each fluid.

Three tracking procedures are available, namely:

• (a) the Volume of Fluid VOF method;
• (b) the scalar-equation SEM method; and
• (c) the height-of-liquid HOL method

click here for a comparison of these methods.

An example from the applications album:

Heavy drop falling through light drop

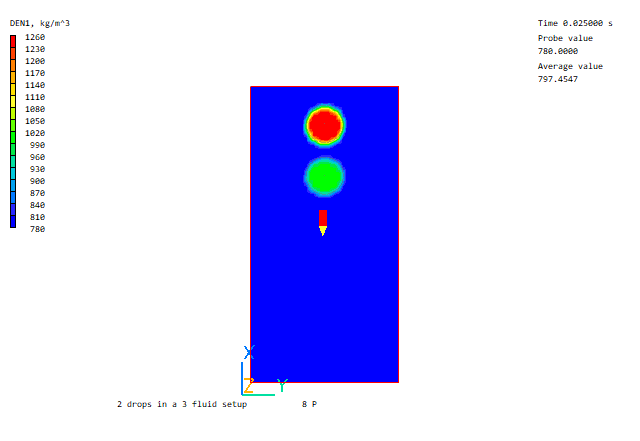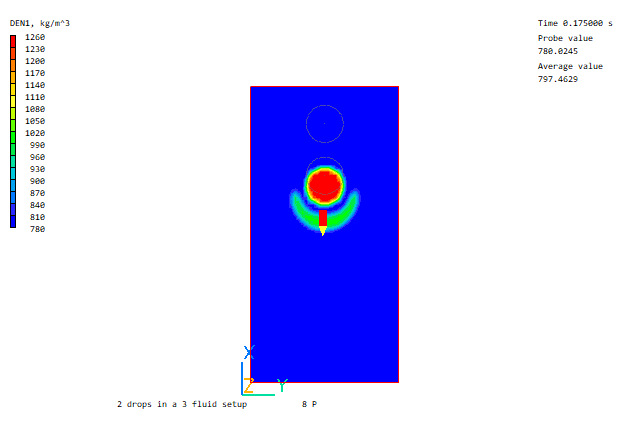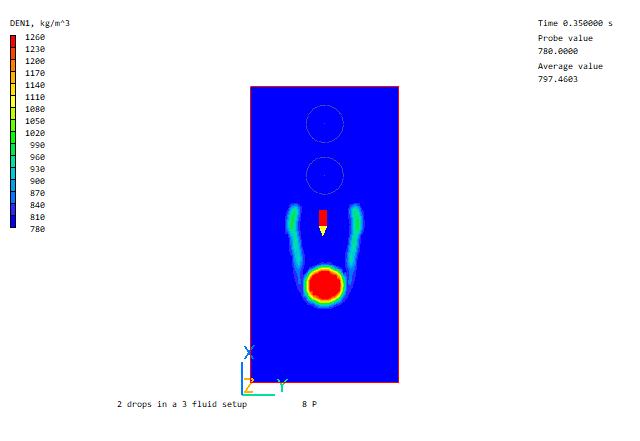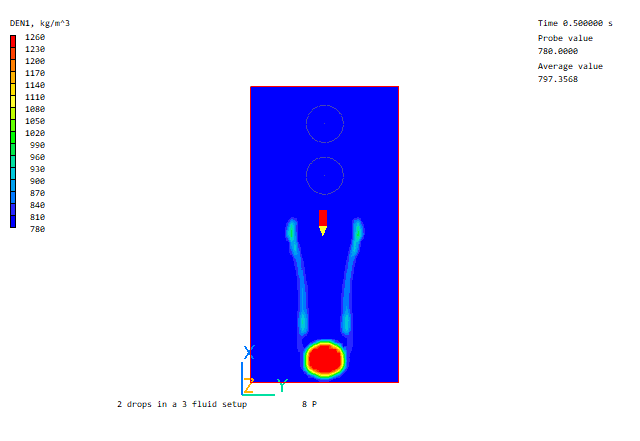
Further Volume of Fluid examples

Method (4): the Lagrangian (i.e.particle-group tracking option)

Method (4) is embodied in the GENTRA (i.e.GENeral TRAcking) option of PHOENICS.

The particles (or groups of particles) are tracked by solving the Lagrangian equations of motion, with full interactivity between the particulate and the continuous phases.

Heat, mass and momentum transfer can take place between the particulate and continuous phases; and the particles can undergo phase change and chemical reaction. They may also radiate.

Allowance is made for the particles to stick to walls which they hit, to slide along them subject to friction, or to bounce off with various coefficients of restitution.

GENTRA has found many applications in chemical engineering, power engineering and aeronautics, e.g.the icing of aircraft-engine intakes.

Examples of the application of the above methods to industrial and scientific flow simulations will be found in the Application Album.

For further information, see the PHOENICS Encyclopaedia entries: IPSA, ASLP, VOF, SEM, HOL, GENTRA, and also the Lectures on PHOENICS at the top level of POLIS.

See also the Encyclopaedia article on Multi-Fluid Models of Turbulence, and the lectures accessible from the top POLIS menu.

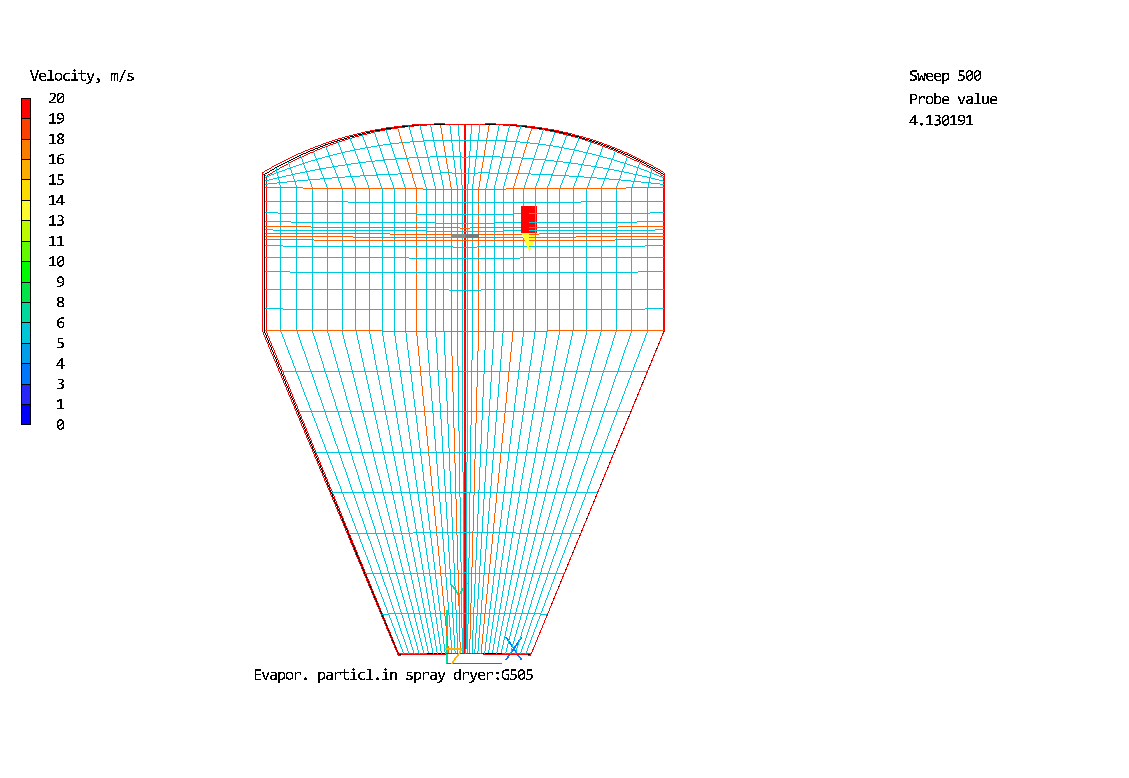Body-fitted grid for a spray dryer

Gas flow field

Particle trajectories

Contours of vaporisation rate

Contours of vapor mass fraction