Multiphase flows are of great practical importance in many common engineering and environmental applications:
Multiphase flows are characterized by two or more fluids in motion relative to each other.
The fluids will also usually have different physical properties - temperature, density, conductivity.
A phase is an identifiable class of material in a mixture. Identifying characteristics may be:
Flows where the phases are not mixed, but are separated by a sharp interface, can be also solved using multiphase techniques.
It is often more efficient to use modified single phase methods, such as the Scalar Equation or Height of Liquid methods.
The rest of this lecture concentrates on interspersed flows.
The prediction of multiphase phenomena involves computation of the values of:
and possibly:
for each phase.
Specific features of the solution procedure are:
This method is embodied in PHOENICS as the Interphase Slip Algorithm, IPSA;
An alternative technique is to track individual particles in a Lagrangian framework. This technique, embodied in GENTRA, is beyond the scope of this lecture.
Each phase is regarded as having its own distinct velocity components.
Phase velocities are linked by interphase momentum transfer - droplet drag, film surface friction etc.
Each phase may have its own temperature, enthalpy, and mass fraction of chemical species.
Phase temperatures are linked by interphase heat transfer.
Phase concentrations are linked by interphase mass transfer.
Each phase can be characterized by a 'fragment size'. This could be a droplet or bubble diameter, film thickness or volume/surface area.
Phase 'fragment sizes' are influenced by mass transfer, coalescence, disruption, stretching etc.
Each phase may have its own pressure - surface tension raises the pressure inside bubbles, and interparticle forces prevent tight packing, by raising pressure.
The task is to provide equations, from the solution of which values of ri, ui, vi, wi, Ti, Ci, and so on can be deduced.
These equations include mathematical expressions for the rates of the interphase transport processes described above. These are sometimes called the 'constitutive relationships'. The expressions are often empirical, and mainly come from experiment.
The equations describing the state of a phase are basically the Navier-Stokes Equations, generalised to allow for the facts that:
The phase continuity is regarded as the equations governing the phase volume fractions. They are the counterparts of the single phase continuity equation.
d(riri)/dt + div( ririVi - Grigrad(ri)
) = ñji
Transient Convection Phase Diffusion Mass
Source
Where:
Notes:
r1 + r2 = 1
The conservation equations for any variable of phase i, f i, read:
d(ririfi)/dt+div(
ririVifi
-riGfi grad(fi)-fiGri grad(ri) ) = Si+Sip
Transient Convection Within-phase and Phase
Diffusion Sources
Where:
Notes:
IPSA has been implemented in PHOENICS for two phases only.
IPSA is activated by placing in the Q1 file the statement:
Alternatively, in the VR-Editor, IPSA is activated from the Models panel of the Main Menu. The IPSA Settings panel allows all the control variables described below to be set. Solution of the required phase 1 and phase 2 variables is then automatic.
The Inlet- and Outlet-object attribute dialogs offer the choice of which phase is to enter or leave.
followed by:
SOLVE(P1, U1,U2, V1,V2, W1,W2, R1,R2, H1,H2, C1,C2, ...)
A numerical technique called the Partial Elimination Algorithm (PEA), is used to procure convergence for tightly-linked variables. By default, the PEA is active between pairs of SOLVEd variables, as shown below:
Phase 1 Variable Phase 2 Variable
Note that all odd numbered variables 'belong' to phase 1, and even numbered variables 'belong' to phase 2.
The TERMS command can be used to switch variables between phases.
Argument 6 is 'Variable belongs to first phase?'.
Thus:
TERMS(C2,P,P,P,P,Y,P)
would switch C2 from its default phase 2 to phase 1.
Inlets
Boundary conditions must be specified for whichever phase is to be affected by the PATCH in question. For mass flow conditions, the practice is to use P1 for phase 1 mass fluxes, and P2 for phase 2 mass fluxes.
A typical inlet specification where both phases are entering the domain is:
INLET(IN, LOW, 1, NX, 1, NY, 1, 1, 1, LSTEP) VALUE(IN, P1, R1in * RHO1in* W1in) VALUE(IN, P2, R2in * RHO2in * W2in) VALUE(IN, W1, W1in) VALUE(IN, W2, W2in)
wherein R1in, R2in are the volume fractions in the incoming stream.
Obviously, R1in + R2in = 1.0.
Outlets
If both phase densities are constant, and both phases can pass in or out, outflows can be simply specified using:
OUTLET(OUT, HIGH, 1, NX, 1, NY, NZ, NZ, 1, LSTEP) VALUE(OUT, P1, Pext) VALUE(OUT, P2, Pext)
- if Pext is not zero.
If only one phase is allowed to pass, then a PATCH must be used, with a COVAL for P1 or P2.
PATCH(OUT, HIGH, 1, NX, 1, NY, NZ, NZ, 1, LSTEP) COVAL(OUT, P1,1E3, Pext)
- if only Phase 1 is allowed to pass
or
COVAL(OUT, P2,1E3, Pext)
- if only Phase 2 is allowed to pass.
Walls
The WALL command assumes that phase 1 is the continuous phase, and will only generate wall functions for this phase. If wall effects are required for phase 2, these have to be explicitly added in.
Note that in the examples above, P2 is only a flag for phase 2 mass sources - it is NOT a 'real' pressure, and it does NOT have to be STOREd or SOLVEd.
For single phase flows, the mass flow associated with a PATCH and COVAL for P1 is:
m' = Type × Cp1 × ( Vp1 - P1 )
where Type is the geometrical multiplier specified through the PATCH type.
In two phase flows, the relationship for P1 (or P2) is:
m' = Type × Cp1 × ( Vp1 - P1 ) for P1 < VPi
{inflows}
m' = Type × R1 × Cp1 × ( Vp1 - P1 ) for P1 > VPi
{outflows}
i.e., it is the same for inflows, but has an additional volume fraction multiplier for outflows. This means that for equal phase COefficients and VALues, outflows are proportional to in-cell volume fraction.
Unfortunately, in many practical cases, outflow is more realistically represented as proportional to in-cell mass fraction. This can be achieved by setting the COefficient to the required COefficient multiplied by the in-cell phase density.
The OUTLET command thus arranges that the COVALs generated are:
COVAL(OUT,P1,1E3,Pext) or COVAL(OUT,P1,RHO1*1E3,Pext)
COVAL(OUT,P2,(RHO2/RHO1)*1E3,Pext) or COVAL(OUT,P2,RHO2*1E3,Pext)
If either RHO is set to a GRND number, both COefficients are set to 1E3, and it is left to the user to arrange for appropriate multiplication, either by average outlet densities in Q1, or by the actual in-cell densities in GROUND.
Within-Phase Diffusion
The normal within-phase diffusion treatment for two phase flow is very similar to the single phase. The diffusion coefficient for each phase is written as:
Gfi = RHOi × ( ENUL / PRNDTL(f) + ENUT / PRT(f) )
The term includes both laminar and turbulent mixing. Note that there is only one laminar and one turbulent viscosity. These are the phase 1 viscosities. If different viscosities are required in the second phase, the Prandtl numbers can be used to introduce the appropriate ratios.
If one of the phases, normally phase 2, is a dispersed one, say droplets or particles, then within-phase turbulent effects are absent. PRT(f) should be set to a large number, say 1E10.
Phase Diffusion
The phase diffusion term accounts for turbulent dispersion of particles or droplets due to turbulence in the continuous phase, and is present in both the phase continuity and phase phi equations. The diffusion coefficient is written as:
Gri = RHOi × ( ENUL / PRNDTL(Ri) + ENUT / PRT(Ri) )
Phase diffusion effects can be removed by setting both Prandtl numbers for both phases to large numbers, say 1E10.
Turbulence Modelling
The turbulence variables, KE and EP, are always phase-1 variables, and the generation rate is calculated from phase-1 velocity gradients. If required, it is possible to modify the GREX coding to switch the turbulence model to phase 2, though this should not normally be necessary.
The presence of particles will normally have a damping effect on the turbulence field. Strictly speaking, this effect is not completely modeled in the built-in k-E model. Only the generation term and dissipation terms are reduced by the volume fraction, but there is no explicit damping. This can be introduced via additional source/sink terms.
Two forms of these terms are provided in the GX routine GXDISP, which is activated by a PATCH whose name starts with 'KEDI'. COef and VALue for KE and EP are set to GRND1,0.0 or GRND2,0.0 to activate the models of Mostafa & Mongia or Chen & Wood respectively.
The interphase source contains the diffusive (e.g., friction, heat transfer) and convective (mass transfer related) links between the phases. It is formulated in the general form as follows.
General Form
SIP=(ff,i+ <mji>) (fiint -fi)
where:
ff,i = interphase (diffusive) transfer
coefficient, kg/s;
mji = net mass transfer rate between the phases, kg/s;
<> = maximum of 0.0 and the quantity enclosed;
fiint = value of f
at the interface between the phases and
fi is a bulk phase value of conserved variable f.
Notes:
SIP,1=(ff,1+ <m21>) (f1int
-f1)
SIP,2=(ff,2+ <m12>) (f2int -f2)
wherein m21 = - m12;
The concept of the interface value

fiint is the value of fi at the i-j interface. It can be a function of space, time, or local bulk phase values. It is a property, and not a variable obtained from a conservation equation.
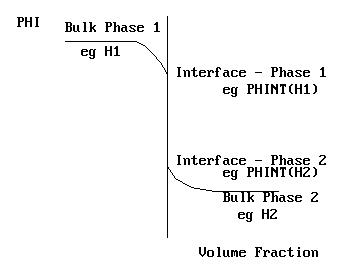
In terms of a steam - water system, PHINT(H1) and PHINT(H2) would represent the saturation enthalpies of steam and water at the local temperature and pressure. The near-interface situation is shown on the picture above.
In the case where CO2 diffuses between water and air, and C1 represents the concentration in the air, and C2 represents the concentration in the water, then PHINT(C1) and PHINT(C2) would represent the concentrations at the air-water interface.
In other cases, interphase momentum transfer for example, the concept of an interface value is not helpful, and it is more meaningful to think of direct transfer between bulk phase values.
Settings for PHINT(f)
The PIL variable controlling fi is PHINT(f). There are many options for setting PHINT values.
¤ Bulk-to-bulk-transfer interface values
In this case, the interface value of current phase is made equal to the bulk value of another phase, i.e.
fiint = fj
Then, interphase source becomes
SIP=(ff,i+ <mji>) (fj -fi)
where:
fi is current phase bulk value of f and
fj is another phase bulk value of f.
¤ Known interface values
If the values of f at the interface between the phases are known, say,
fiint = Value1 and
fjint = Value2
interphase source becomes
SIP=(ff,i+ <mji>) (Valuei-fi)
Notes:
¤ Known difference in interfacial values.
If the difference in values of f is known at the interface between the phases, say,
diff = fiint - fjint
the actual interface values can then be expressed via phase bulk values as
fiint = fj
+ diff
fjint = fi
- diff
and resulting interphase source becomes
SIP=(ff,i+ <mji>) (fj - fi + diff)
¤ Known ratio of interfacial values.
If the ratio of f values is known at the interface between the phases, say,
Value1 = fiint/ fjint
the actual interface values can then be expressed via phase bulk values as
fiint = Value1 × fj
fjint = fi/Value1
and resulting interphase sources become
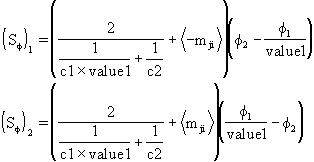
where:
C1 and C2 are bulk-to interface transfer coefficients to be defined in the following considerations.
ff,i, kg/s, featured in SIP is actually the interphase flux per cell per unit conserved variable difference.
For built-in treatment, the specific interphase fluxes are made proportional to fIP, which is termed the reference interphase transfer coefficient.
fIP or FIP, kg/s=Ns/m, is the force per cell per unit velocity difference.
It appears as multiplier, in the built-in formulations of all specific ff,i and mji. This multiplier is introduced because of the analogy between friction, heat and mass transfer.
The coefficient fIP is controlled by the PIL variable CFIPS.
If CFIPS is any constant other than a GRND flag, fIP is set as follows:
fIP = CFIPS×RHO1×R1× R2*×Vol, for CFIPS >0.0
fIP = |CFIPS|×RHO2×R2× R1*×Vol, for CFIPS <0.0
In the above, Ri* is the maximum of Ri and RLOLIM. This ensures that, as long as RLOLIM > 0.0 , the reference interphase transport coefficient remains finite, even though the volume fraction of either phase falls to zero. Vol is the cell volume.
This has reasonable consequences when friction is concerned, as it ensures that very small bubbles travel at the same velocity as the carrying liquid.
Ignoring the interphase mass transfer, for bulk-to-bulk transport of momentum, the interphase source term becomes:
SIP =fIP × ( velj - veli)
where SIP has units of Newton and fIP is now the interphase drag coefficient between phases in units of Ns/m or kg/s. CFIPS of the above options,in units 1/s, is now proportional of the product of phase slip velocity and projected area per unit volume.
If STORE(CFIP) is set in the Q1 file, then fIP is stored for output purposes, and also for under-relaxation purposes via the RELAX command.
The built-in options provided are described fully under the Encyclopaedia entries CFIPS and INTERPHASE DRAG MODELS , and so only a brief description of the major ones will be provided here.
fIP =0.75 ×Cd×RHO1×R2×R1* ×Vol×<Vslip,CFIPA> / Dp
wherein phase 1 is the carrier and phase 2 is dispersed.
Here, CFIPA is a parameter used to define the minimum value allowed for slip velocity , Vslip, between the phases, Cd is a dimensionless particle drag coefficient and Dp is the particle diameter (defined by CFIPB).
The PIL variable CFIPD selects the Cd correlation:
= 0 - Standard drag curve (default)
= 1 - Stokes-regime drag correlation
= 2 - Turbulent-regime drag correlation
= 3 - Subcritical-regime drag correlation
= 4 - Distorted-bubble "dirty-water" drag correlation
= 5 - Spherical-bubble "dirty-water" drag correlation
= 6 - Ellipsoidal-bubble "clean-water" drag correlation
Notes:
fIP = 0.75×RHO2×R1×R2*×Vol× <Vslip,CFIPA> / Dp
Notes:
In many cases, the driving force is the temperature difference and available heat transfer correlations are based upon it.
With solving for enthalpies, H1 and H2 and ignoring mass transfer the interphase sources become:
SH1 = h12 × AS × (T1int - T1)
SH2 = h21 × AS × (T2int - T2)
where:
h12 = bulk1-to-interface heat transfer coefficient, W/m2K
h21 = bulk2-to-interface heat transfer coefficient, W/m2K
AS = total interface area, m2
The interface temperatures, T1int and T2int, can be eliminated via overall heat transfer coefficient and bulk-to-bulk temperature difference as follows:
SHi = 1 × AS × (Tj - Ti)/(1/C1 - 1/C2)
where: C1 = hij and C2 = hji
This formulation is generalised so that the interphase transfer coefficient, fIP, is taken to be harmonic average of the bulk-to-interface coefficients, C1 and C2.
Thus,
fIP = 2 / (1/C1 - 1/C2)
Note: if C1 = C2 = C, then fIP = C
Built-in provisions have been made to calculate C1 and C2 via their ratios to the reference transfer coefficients, as follows
C1 = CINT(f1) × FIP
C2 = CINT(f2) × FIP
Notes:
In PHOENICS two-phase mode, it is common to solve for enthalpy. It is required a source, in Watts, in the form:
SHi = hij × AS × (Tj - Ti)
where:
For the particulates of spherical shapes of diameter Dp, their surface area is given by
AS = 6 × R2 × Cell Volume / Dp
The heat transfer coefficient is then computed from the local Nusselt Number, Nu = hij × Dp/k, thus
hij = k × Nu / Dp, where
k = heat conductivity of the carrier phase, W/mK.
Two options for computing Nu have been provided in PHOENICS.
Notes:
Two variants of CINT(Hi) =GRND7 or GRND8 deal with phase specific heats as follows:
The interphase mass transfer rate, mji in kg/s, is controlled by the PIL variable CMDOT, as follows:
mji = CMDOT × fIP
where fIP or FIP = the reference interphase transfer coefficient, kg/s.
Notes:
Two built-in options provided for the calculation of mji:
The virtual- (also called "added-") mass term in the momentum equations for dispersed two-phase flow represents the force required to accelerate the mass of the surrounding continuous phase, in the immediate vicinity of a dispersed-phase fragment, such as a bubble or droplet, when the relative velocity of the phases changes.
It is significant only if the continuous-phase density is of the same order of magnitude as ,or much greater than, that of the dispersed phase, as for water droplets in oil or for steam bubbles in water.
Otherwise, as for sand particles in air or for water droplets in steam (at pressure well below the critical), the virtual-mass effect may be neglected.
Formulation
PHOENICS employs the Drew and Lahey (1987) formulation whereby the following source terms are introduced on the right-hand sides of the two momentum equations:
Sc = rC × Cvm × rd
× avm
Sd = - Sc
wherein:
rc = the local density of the continuous phase,
kg/m3;
Sd and Sc = the volumetric force vectors for continuous, c, and
dispersed, d, respectively, N/m3;
Cvm = the virtual mass coefficient;
rd = the volume fraction of phase d and
avm = the virtual-mass acceleration vector, m/s2;
Activation
The virtual-mass sources for the momentum equations are activated by assigning a non-zero value to the PIL variable CVM. The value ascribed to CVM determines how the virtual-mass coefficient is to be calculated, as follows:
Notes
Interphase friction, heat transfer and mass transfer rate
The recommended method of introducing non-standard correlations for dilute ( R2<<R1 ) suspensions is:
FIP = 0.75×Cd×RHO1×R2×Volume× Vslip / Dp
Where:
Cd = dimensionless drag coefficient
RHO1 = density of continuous phase, kg/m3
R2 = volume fraction of dispersed phase
Volume = unblocked volume of the cell, m3
Vslip = relative velocity of the phases, m/s
Dp = particle diameter, m
CINT(H1) = GRND and
CINT(H2)=GRND
PHINT(H1)=CP1/CP2
CINT(H1)=CINT(H2)=Ci with
Ci = (k·Nu/Dp)·(6·R2/Dp)·Volume·(CP1+CP2)/(2·CP1·CP1)
or
CINT(H2) = 1.e20 and
CINT(H1) = (k·Nu/Dp)·(6·R2/Dp)·Volume/(2·CP1)
Where:
k = heat conductivity of continuous phase, W/(mK)
Nu = dimensionless local particle Nusselt number
CP1 = continuous phase specific heat, J/(kgK)
CP2 = dispersed phase specific heat, J/(kgK)
Note:
Virtual-mass coefficient
If CVM is set equal to GRND in Q1 the user can supply his/her own formula for Cvm.
It should be done in Group 10 Section 5 of GROUND.
For example, the FORTRAN lines
CALL SUB2(L0CVM,L0F(LD12),L0R2,L0F(R2))
DO 1052 I-1,NXNY
F(L0CVM+I)=CVMA*(1.-2.78*AMIN1(0.2,F(L0R2+I)))
1052 CONTINUE
provide the instructions to compute Cvm identically to what is provided in option CVM=GRND2.
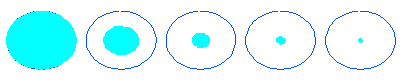
Dp / Dp,in = ( R2 / RS )1/3
Examples of two-phase flow can be found in the following sections of the Library.
On the SHADOW volume-fraction technique:
On interphase drag laws and heat/mass transfer coefficients:
On turbulence modulation by particles:
About multiphase flow in general:
On Basic Equations of Two-Phase Flow:
On IPSA:
svz/331/0201
jcl/351/0903