An Overview of ESTER
URPOSE OF DOCUMENT
The purpose of this document is to provide basic information regarding ESTER, and the limitations and assumptions made. The reader is assumed to have a working knowledge of PHOENICS, and a much higher degree of familiarity with Hall Cells.
2. G
ENERAL INFORMATIONESTER (Electrolytic SmelTER) is a Special Purpose adaptation of the general purpose fluid flow and heat transfer code PHOENICS. It is attached to PHOENICS as an additional GROUND station. It makes use of the standard PHOENICS pre- and post-processors for data input and graphical display. From PHOENICS 1.6.5, ESTER is included as part of the standard package, together with example input files. The ESTER example library is in:
/phoenics/d_earth/d_spe/d_ester/inplib/ulib.
Back to Top3. T
HE EQUATIONS SOLVEDESTER solves the steady state or transient fluid flow and electric potential distributions within an aluminium reduction cell, of the Hall Cell type. The equations solved are pressure, P1, three velocity components U1, V1 and W1, and the electric potential EPOT. The height of the metal-electrolyte interface is adjusted periodically to maintain hydrostatic equilibrium across the interface.
A very simple turbulence model is used - a constant effective viscosity is specified. The standard PHOENICS
k -e model can easily be activated if preferred. It is also straightforward to activate the solution of equations for temperature and aluminium oxide concentration.The two-phase option of PHOENICS can be activated to model the dispersion of gas bubbles from the anode undersides, through the inter-anode and anode-wall gaps.
Back to Top4. M
ATHEMATICAL BASIS4.1 Solution of The General Conservation Equation
PHOENICS solves a general conservation equation, which for a single phase flow may be written as:
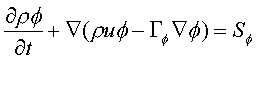
where:
f - the conserved quantity eg momentum, energy, mass etc.
r - density
u -- velocity vector
G f - diffusive exchange coefficient
S
f - source termThe source term and exchange coefficient vary from equation to equation, and also from case to case. Examples of source term are pressure gradient and gravity force for the momentum equations, or kinetic heating for the enthalpy equation. The mass continuity equation can also be written in the above form by setting
f =1 and G fThe commonly appearing sources, such as those mentioned above, are pre-programmed into the PHOENICS solver, EARTH. Provision is then made to enable users to add in any further sources required.
The partial differential equation above is integrated over 'control volumes' (cells) to form the Finite Volume Equation actually solved. The linkage between velocity, pressure and continuity is resolved by a variant of the SIMPLE algorithm.
4.2 Momentum Sources
In a Hall Cell, the flow is primarily driven by the Lorentz forces. These are added to the standard momentum equations through the ESTER Ground station.
The Lorentz forces are computed from the cross product of the electric current, J, and the magnetic field, B.
F = J x B
In terms of x y and z components, this is:
Fx = Jy * Bz - Jz * By
Fy = Jz * Bx - Jx * Bz
Fz = Jx * By - Jy * Bx
These forces are then applied to the momentum equations as source terms.
Laminar friction is applied at the cathode, and on the anode undersides.
4.3 The Potential Equation and Current Calculations
The potential equation is obtained from the standard conservation equation by removing the built-in sources, and convective and transient terms. The remaining, diffusive, term then contains the electrical conductivity.
Finally, the currents are deduced in the Ground station as the gradients of the electric potential:
J = - s Ñ E
In terms of x y and z components, this is:
Jx = -s * (Ee-Ep)/DXG
Jy = -s * (En-Ep)/DYG
Jz = -s * (Eh-Ep)/DZG
where DXG, DYG and DZG are the distances between cell centres in the x, y and z directions.
In addition, the induced currents arising from the motion of the liquid through the magnetic field are calculated from:
Ji = s ( V x B )
In terms of x y and z components, this is:
Jix = s * (V * Bz - W * By)
Jiy = s * (W * Bx - U * Bz)
Jiz = s * (U * By - V * Bx)
The total current is then J + Ji. The calculation of Ji is controlled by the variable LG(1). When set to T, the induced currents are calculated, when left at F, they are not.
The potential, being a scalar, is stored at the cell centres. The currents, being components of a vector, are stored at the cell faces. This results in complications at the Lorentz force stage, as none of the currents is stored at a convenient location. Hence in the calculation of the Lorentz force, for each current component four currents must be averaged to the relevant cell face, taking into account non-uniformities of the grid.
4.4 Potential Equation Sources
The boundary conditions for the potential equation are:
This is equivalent to fixed mass flux and fixed pressure respectively.
The cathode current can either be set to a constant value, or a distribution can be read in from a file containing cell by cell values over the cathode. It is left to the user to specify these values appropriately. The values should be specified in amps/m2.
Note that if freeze is present, the cathode currents under the freeze should be set to zero. The freeze is a very poor conductor, and huge potentials will result. These may lead to numerical overflow.
The setting of cathode current is controlled by the variable JZCATH. This can take the following values:
logical unit JZCATH.
If CG(2) is set to Q1, the data can be included in Q1, starting in column 3 or more. The start of the data is marked with *JZC in column 3.
The anode potential is presently set to a single constant value in all anodes.
This is done in the subroutine POTENT, which is supplied as a model. If the user wishes to update anode potentials, then POTENT can be used as a 'junction box', to interface to some other software suite which would supply the potentials.
The potential is set at the centre of the high face of the top slab of the domain.
A further source for the potential equation arises from the induced currents. This source takes the form:
S = Ñ Ji
This is written in finite-difference form as:
S = (An.Jiy)p - (An.Jiy)s + (Ae.Jix)p - (Ae.Jix)w + (Ah.Jiz)p -(Ah.Jiz)l
where the subscript 'p' denotes the current cell, and 'w','s','l' denote the neighbours in the low x, low y and low z directions. Ae, An and Ah are the cell face areas.
If the induced currents are not calculated, i.e. LG(1)=F, the source is set to zero.
4.5 Magnetic Fields
To avoid the interpolation complications associated with the current components, the B field components are deemed to be stored at the cell centres, even though they too are strictly vectors. The values of Bx, By and Bz can either be calculated from simple algebraic expressions, or individual cell values can be read in from a data file. The fields should be specified in Gauss.
There is at present no provision for updating the B field, but this can easily be done from Group 19 of the Ground station, if a suitable physical mechanism is known.
The setting of the B field is controlled by the variable MAGF. This can take the following values:
the ESTER Ground station.
If CG(1) is set to Q1, the data can be included in Q1, starting in column 3 or more. The start of the data is marked with *MAGF in column 3.
4.6 Location of Anodes
The locations of the anodes are read in from a data file. The file contains a 0 or a 1 for each cell on a slab. Zero means no anode, one means anode present for IZ > IZ2 up to IZ = NZ.
|-----------------| NZ
Anodes | |XXX| |XXX| |
| |XXX| |XXX| |
| |XXX| |XXX| | ^
|-----------------| |
| | | | | | IZ2 |
| | | | | | | iz
Interface |-----------------| |
| | | | | | IZ1 |
| | | | | | |
| | | | | | |
| | | | | | |
Cathode |-----------------| 1
IZ1 denotes the slab immediately under the metal-electrolyte interface, IZ2 denotes the slab immediately under the anodes, and IZ3 denotes the slab immediately under the electrolyte-air interface. Normally IZ3=NZ, as the air space is not considered. If it is, then only potential calculations within the anodes are performed.
All velocities are set to zero inside the anodes, and the pressure is set to zero. Only the potential equation is solved inside the anodes.
The reading of the file is controlled by the variable IANO. This can take the following values:
IANO.
If CG(4) is set to Q1, the data can be included in Q1, starting in column 3 or more. The start of the data is marked with *IANO in column 3.
The underside of the anodes, ie the high faces of slab IZ = IZ2, may be flat, or a non-uniform distribution may be read in from a data file.
The reading of the file is controlled by the variable HANO. This can take the following values:
logical unit HANO.
If CG(5) is set to Q1, the data can be included in Q1, starting in column 3 or more. The start of the data is marked with *HANO in column 3.
Under some circumstances, the anode undersides may take on the shape of the metal-electrolyte interface. This situation, known as 'burn-off', may be modelled by setting LG(4) = T. The distance between the anodes and the interface will now be kept constant at the initial value irrespective of the motion of the interface.
4.7 Freeze
The freeze is the solid accretion around the edges of the cell, which reduces the volume and the available cathode area. The presence of freeze is accounted for by fixing the velocities and pressure to zero in selected cells. The potential is also fixed to zero within the freeze, as it is such a poor conductor.
The location and height of the freeze is read in from a data file. The file contains the height, in full Z slabs, of freeze in each column of cells. The freeze may extend up into the electrolyte layer.
The reading of the file is controlled by the variable IFRZ. This can take the following values:
IFRZ.
If CG(3) is set to Q1, the data can be included in Q1, starting in column 3 or more. The start of the data is marked with *IFRZ in column 3.
The modelling of the freeze is very simple - no partial cell occupation is allowed, and freeze will rise and fall with the interface, as the height is specified in terms of slabs, not actual height.
4.8 The Moving Grid and the Metal-Electrolyte Interface
A primary feature of the Hall Cell is the presence of two distinct layers of fluid, which never intermingle. The liquid metal is at the bottom, in contact with the cathode. The upper layer is the electrolyte, into which are immersed the anodes.
The Lorentz forces driving the flow cause pressure differences across the interface, which then deforms. The enormous difference in conductivity between metal and electrolyte means that even small changes in interface height can significantly alter the resistance paths, and hence current distributions. This then feeds back to the Lorentz forces and the height distribution.
In ESTER, the interface is always maintained at the high faces of the slab IZ = IZ1. The grid is then stretched to follow the motion of the interface. The grid itself does not actually change, but the North and East porosities, and the z direction internodal distances, are adjusted to give the same effect. This is considerably cheaper computationally than using a distorting BFC grid.
The interface adjustment is based on the principle of maintaining hydrostatic equilibrium across the interface. A reference cell is chosen (the first unblocked cell), and height adjustments are calculated for all other cells based on the pressure difference between the reference cells above and below the interface. Once the adjustments have been applied, the whole interface is moved up or down by a uniform amount in order to preserve the open volume under it.
The adjustment sequence is entered every NIH sweeps, once ISWEEP > IHF.
A similar adjustment can be performed at the electrolyte free surface, where the inter-anode gaps are open to the atmosphere. This can be switched on by setting LG(2) = T.
The vertically directed components of the Lorentz force can be included in the balance equation across the interface by setting LG(3) = T.
The true (i.e. distorted) heights of the cell faces are stored in the variable HI. A PHOTON contour map of the interface can thus be obtained by plotting contours of HI at IZ = IZ1. It is best to SET CON SCALE PLANE prior to this, as the changes in height on a plane are usually very small.
HE FILE STRUCTUREThe files making up ESTER have the following significances:
1 1 1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 1
^ 1 0 0 0 0 0 0 0 0 1
IY | 1 0 0 1 1 0 0 0 0 1
| 2 1 1 1 1 1 1 1 1 1
|____>
IX
0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. -5000. -5000. -5000. -5000. -5000. -5000. -5000. -5000. 0.
0. -5000. -5000. -5000. -5000. -5000. -5000. -5000. -5000. 0.
0. -5000. -5000. -5000. -5000. -5000. -5000. -5000. -5000. 0.
0. -5000. -5000. -5000. -5000. -5000. -5000. -5000. -5000. 0.
0. -5000. -5000. -5000. -5000. -5000. -5000. -5000. -5000. 0.
0. -5000. -5000. -5000. -5000. -5000. -5000. -5000. -5000. 0.
^ 0. -5000. -5000. -5000. -5000. -5000. -5000. -5000. -5000. 0.
IY | 0. -5000. -5000. 0. 0. -5000. -5000. -5000. -5000. 0.
| 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
|---> IX
0 0 0 0 0 0 0 0 0 0
0 1 1 1 0 0 1 1 1 0
0 1 1 1 0 0 1 1 1 0
0 1 1 1 0 0 1 1 1 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 1 1 1 0 0 1 1 1 0
^ 0 1 1 1 0 0 1 1 1 0
IY | 0 1 1 1 0 0 1 1 1 0
| 0 0 0 0 0 0 0 0 0 0
|____>
IX
0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260
0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260
0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260
0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260
0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260
0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260
0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260
^ 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260
IY | 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260
| 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260
|____>
IX
An alternative set of data shown below, indicates how sloped anodes may be introduced. This data should be used for 2-phase calculations, as the gas will tend to move up the slopes towards the central inter-anode gap and then escape.
0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260
0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260
0.267 0.267 0.267 0.267 0.267 0.267 0.267 0.267 0.267 0.267
0.274 0.274 0.274 0.274 0.274 0.274 0.274 0.274 0.274 0.274
0.274 0.274 0.274 0.274 0.274 0.274 0.274 0.274 0.274 0.274
0.274 0.274 0.274 0.274 0.274 0.274 0.274 0.274 0.274 0.274
0.274 0.274 0.274 0.274 0.274 0.274 0.274 0.274 0.274 0.274
^ 0.267 0.267 0.267 0.267 0.267 0.267 0.267 0.267 0.267 0.267
IY | 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260
| 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260 0.260
|____>
IX
DO IX=1,NX
READ() (Bx(IY,IX),By(IY,IX),Bz(IY,IX),IY=1,NY)
ENDDO
Back to Top6. P
OSSIBLE EXTENSIONSThe following extensions to ESTER are suggested: